ギャンブルの期待値とは？計算方法や活用方法をわかりやすく解説

ギャンブルでは「期待値」という概念があります。期待値を正しく計算することは、ギャンブルで勝つために重要です。ここでは、ギャンブルの期待値とはそもそも何なのか、また計算方法や活用方法について、詳しく解説しました。

ギャンブルの期待値とは？

ギャンブルの期待値とは、1回賭けた時に何円の利益（損失）が出るのかを表す見込み値です。

期待値がプラスなら、賭けると利益が期待できます。一方で、期待値がマイナスなら、賭けると損失が出ることが予想されます。

しかし、期待値がプラス100円のギャンブルでも、1回賭ければ必ず100円の利益が出るというわけではありません。あくまでも平均的な見込み値です。

例えば1万人が期待値プラス50円のギャンブルで100円ずつ賭けた場合、賭け金額は合計で100万円、全員の利益額を合計すると50万円になります。しかし、その内訳までは分かりません。

ギャンブルの期待値の計算方法

ギャンブルの期待値の計算方法を詳しく解説します。

通常の期待値の計算方法

まずはかなりシンプルなゲームの期待値の計算方法を紹介します。

例えば、コインが1枚あり、これを投げて表が出れば1500円もらえる、裏が出れば300円もらえるとしましょう。この時、期待値を計算する式は以下の通りです。

期待値＝（表が出る確率×表が出た時の賞金額）＋（裏が出る確率×裏が出た時の賞金額）

表が出る確率と裏が出る確率は、それぞれ50％です。

表が出る時の期待値	1500円×50％＝750円
裏が出る時の期待値	300円×50％＝150円

期待値を計算する時は、すべてのパターンの期待値を合算します。つまりこのケースだと、750円＋150円＝900円が期待値です。

仮にこのゲームの参加費が500円だとすると、期待値の方が大きい（900円ー500円＝400円）ため、利益を得る可能性が高いと言えます。

一方でこのゲームの参加費が1,000円だとすると、期待値よりも参加費の方が大きい（900円ー1000円＝ー100円）ので、損する可能性が高いと言えます。

ギャンブル特有の期待値の計算式

ギャンブルには「オッズ」があり、これが還元率の計算を難しくしています。的中時の賞金額は、上記のコインゲームのように、一定ではありません。まず、ギャンブルの期待値の計算式は以下の通りとなります。

期待値=オッズ×賭けた金額×的中する確率

また、ギャンブルでは複数に同時に賭けることもあります。その場合は、すべてのパターンの期待値を合計すればOKです。具体的には、以下の式で計算します。

期待値=（オッズ×賭けた金額×的中する確率）＋（期待値=オッズ×賭けた金額×的中する確率）＋・・・＋（期待値=オッズ×賭けた金額×的中する確率）

期待値の計算例①：1つだけに賭けるケース

賭け金額	1000円
オッズ	6倍
的中する確率	20％

オッズ、的中確率、賭け金額を掛け合わせて計算する
期待値＝6倍×1000円×20％＝1200円

この場合、1000円賭けた時の期待値が1200円ということです。賭け金額よりも期待値の方が上回っているため、確率は20％で高くありませんが、長期的な観点でみると利益を出せる可能性が高いギャンブルと言えます。

期待値の計算例②：2つに賭けるケース

賭け金額	A:1000円 B:700円
オッズ	A:15倍 B:18倍
的中する確率	A:20％ B:8％

2つに同時に賭けるケースでの期待値の計算は以下の流れです。

この時合計の賭け金額は1700円（＝1000円＋700円）です。賭け金額よりも期待値の方が大きいので、賭けると利益が出る可能性が高いと判断できます。

期待値の計算例③：3つに賭けるケース

賭け金額	A:1000円 B:700円 C:500円
オッズ	A:2倍 B:7倍 C:10倍
的中する確率	A:45% B:12％ C:8％

ギャンブルは分散投資が推奨されています。そのため、3つ以上に同時に賭けるケースもあります。しかし、計算方法は同じです。

合計投票金額2200円（＝1000円＋700円＋500円）に対して、期待値は1888円です。期待値の方が投票金額よりも小さいため、この賭け方は損失が出る可能性が高いと判断できます。

的中する確率（外れる確率）は自分で見積もる

ギャンブルの期待値計算が難しい理由として、賭け対象の発生確率が決まっていないことも挙げられます。例えば、コインを投げるゲームなら、表と裏が出る可能性はそれぞれ50％です。サイコロを転がすゲームなら、各数字の目が出る確率は16.7%ずつです。

しかし、法的に認められているギャンブル（公営ギャンブル）では、それぞれの発生確率は決まっていません。

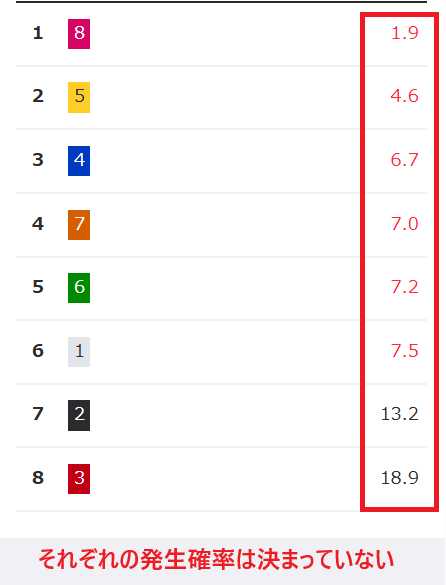
そのため、発生確率は自分自身で見積もる必要があります。適正な発生確率を見積もるためには、過去の実績やレース場と選手の相性、その日の天候など、様々な要因を考慮する必要があります。

この確率をどのくらいの数字で見積もるかによって、期待値は大きく変動します。

的中確率はオッズの値から概算できる

的中確率を自分ですべて見積もるのは、かなり大変な作業です。そこで1つの参考として、オッズの値を活用する方法をおすすめします。

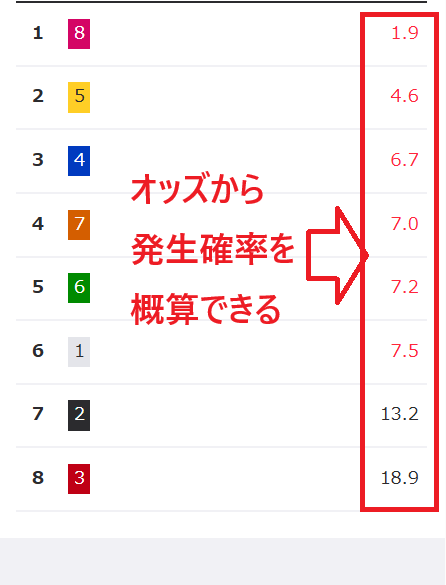
オッズを使ったおおよその的中確率の計算方法は、以下の式を使ってください。

的中確率＝1÷オッズ×100

オッズの例	的中確率
3倍	的中確率＝1÷3×100＝33.3%
5倍	的中確率＝1÷5×100%＝20％

しかし、これはあくまでも参考程度です。まずはオッズを使って的中確率を概算したら、その後自分の調査や分析結果も踏まえて再計算することで、確率を見積もる精度が高くなります。

ギャンブルで期待値を活用する方法

ギャンブルでは、期待値をうまく活用することが大切です。おすすめの活用方法をまとめました。

• 期待値がプラスの時だけ投票する
• 期待値の大きさに応じて賭け金額を調整する（ケリー基準）
• 確率はAI予想を参考にする

それぞれ詳しく解説します。

期待値がプラスの時だけ投票する

基本的には期待値（期待値ー賭け金額）がプラスの時だけ投票しましょう。期待値がプラスなら、利益を出せる可能性が高いと判断できます。

逆に、期待値がマイナスだと損失が出る可能性が高いため、なるべく避けるのがおすすめです。

期待値の大きさに応じて賭け金額を調整する（ケリー基準）

期待値を活用した賭け方に、「ケリー基準」という方法があります。ケリー基準は、期待値の大きさに応じて賭け金額を増減させ、利益の最大化を狙うものです。

例えば、期待値が100円と1000円のレースがあるとしましょう。100円の期待値はやや小さいため、賭け金額は少なめにします。1000円の期待値は大きいので、賭け金額を多めにします。

期待値が高い要因には、発生確率が高いことが挙げられます。つまり、ある程度リスクを負って大きく賭けても問題ないという考え方です。

確率はAI予想を参考にする

発生確率を考えるのが難しいと感じる人は、各投票サイト等で公開されているAI予想を参考にするのもおすすめです。

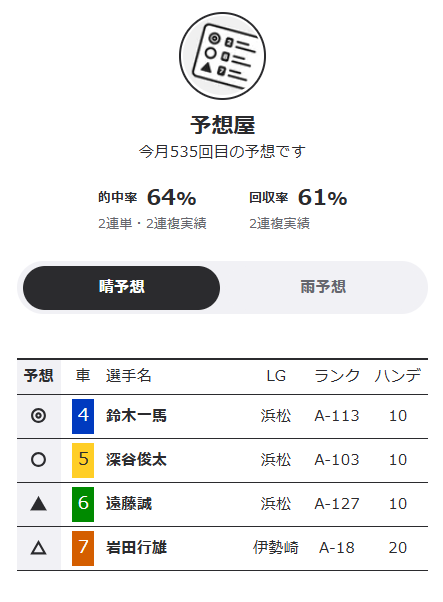
AI予想ツールによっては、回収率や的中率の成績が公開されています。このうち的中率の成績に注目して、高い的中率を記録しているAIツールがおすすめしている予想は、発生確率を少し加点するというやり方です。

例えば、オッズ20倍だと理論上の発生確率は5％（＝1÷20倍×100%）です。しかしこの予想を的中率70%のAI予想ツールがおすすめしているなら、3％分発生確率を上乗せするというイメージです。

※実際に的中率が何％で、どのくらい発生確率を上乗せするかは、自分で基準を決めておく必要があります。一般に50％以上なら的中率は高いと言えるので、的中率50％未満は上乗せなし、的中率50％以上は的中率が10％増えるたびに発生確率を1％ずつ上乗せするという要領でルール決めをすると良いでしょう。

AIツールは過去の膨大なレース結果から予想をしているため、信頼性は高いです。無料で使えるものも多いので、うまく期待値計算にも使えるようになると、ギャンブルの成績が上向いていくことも期待できます。